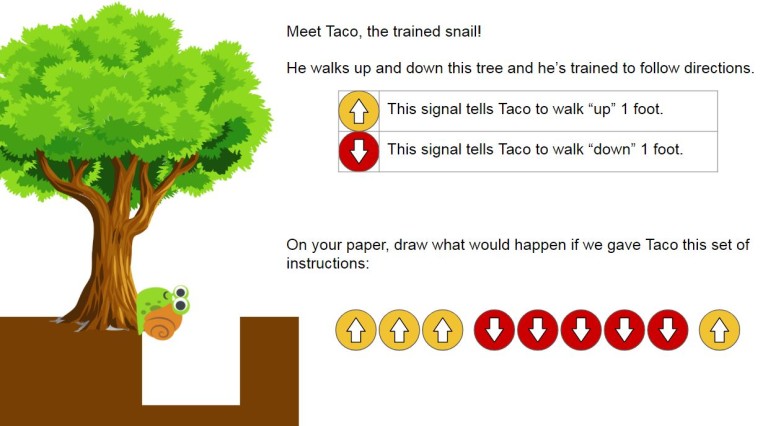
Meet Taco, my trained snail. I give him signals, and he walks up and down a tree in my backyard.
If you’ve worked with integer tiles, you can see some quick connections. The yellow commands look like positive integer tiles, and the red commands look like negative integer tiles. After students experiment with Taco the snail, they are ready to reach some conclusions:
- It doesn’t matter what order the instructions are given.
- Each pair of “up” and “down” erase each other.
Once students have formalized these rules, we can represent them with colored counters, then with numbers and symbols. Eventually, when students are comfortable, they might even write number sentences like: 3 + -5 + 1. When they are ready.
Imagine trying to go backwards through this process. If we began by writing the bare number sentence on the board: 3 + -5 + 1, then pose a list of rules and sample problems, many 6th graders struggle. If we then pull out the integer chips, students are more confused. Students are now processing new rules (that have no context) and trying to make sense of the analogy of these colored manipulatives. Once you’ve shown students a list of rules, you have short-circuited the concept-building, and you can’t “un-ring” that bell.
You have moved AWAY from the math to a manipulative.
Next, if students still struggle, the teacher might offer up a story or some context: imagine you have some money and owe someone money (or check out this trained snail that climbs trees). But this also moves you further away from the math in an attempt to build understanding.
If you start your exploration with the context (meet Taco the snail) and move from concrete explorations, to representational work, then to abstract work, you are continually moving closer to the math. As students are ready, you are introducing more efficient, more accurate algorithms.